Cyclic Voltametry

This document was written by Heather Lukas and Justin Bois.

Background

Electrochemistry is an important family of analytical techniques with applications ranging from renewable fuel cells to medical diagnostics. Cyclic voltammetry is the most widely used technique for acquiring qualitative information about electrochemical reactions and is often the first experiment performed in an electroanalytical study. From cyclic voltammetry, one can study the charge transfer kinetics of a reaction, characterize the behavior of an electrode material, and determine the concentration of a specific analyte in a solution. At the foundation of cyclic voltammetry, a range of voltages is applied to a working electrode and a resulting current is measured based on the redox reaction occurring in solution.

Voltammetry

The three main branches of electrochemistry are potentiometry, Coulometry, and voltammetry. (There are of course specialized techniques like amperometric titration and electrogravimetry.) Voltammetry is the measurement of current as a function of applied voltage to study a chemical analyte. It dates back to the 1920s, evolving more generally from one of many voltammetic techniques called polarography, for which Jaroslav Heyrovský won the Nobel Prize.

There are many voltammetric methods in wide use, differing mainly in how the applied voltage varies over time, how the analyte solution is mixed (if at all), and in the shape and movement of the electrodes. Almost all methods have a basic setup sketched below.

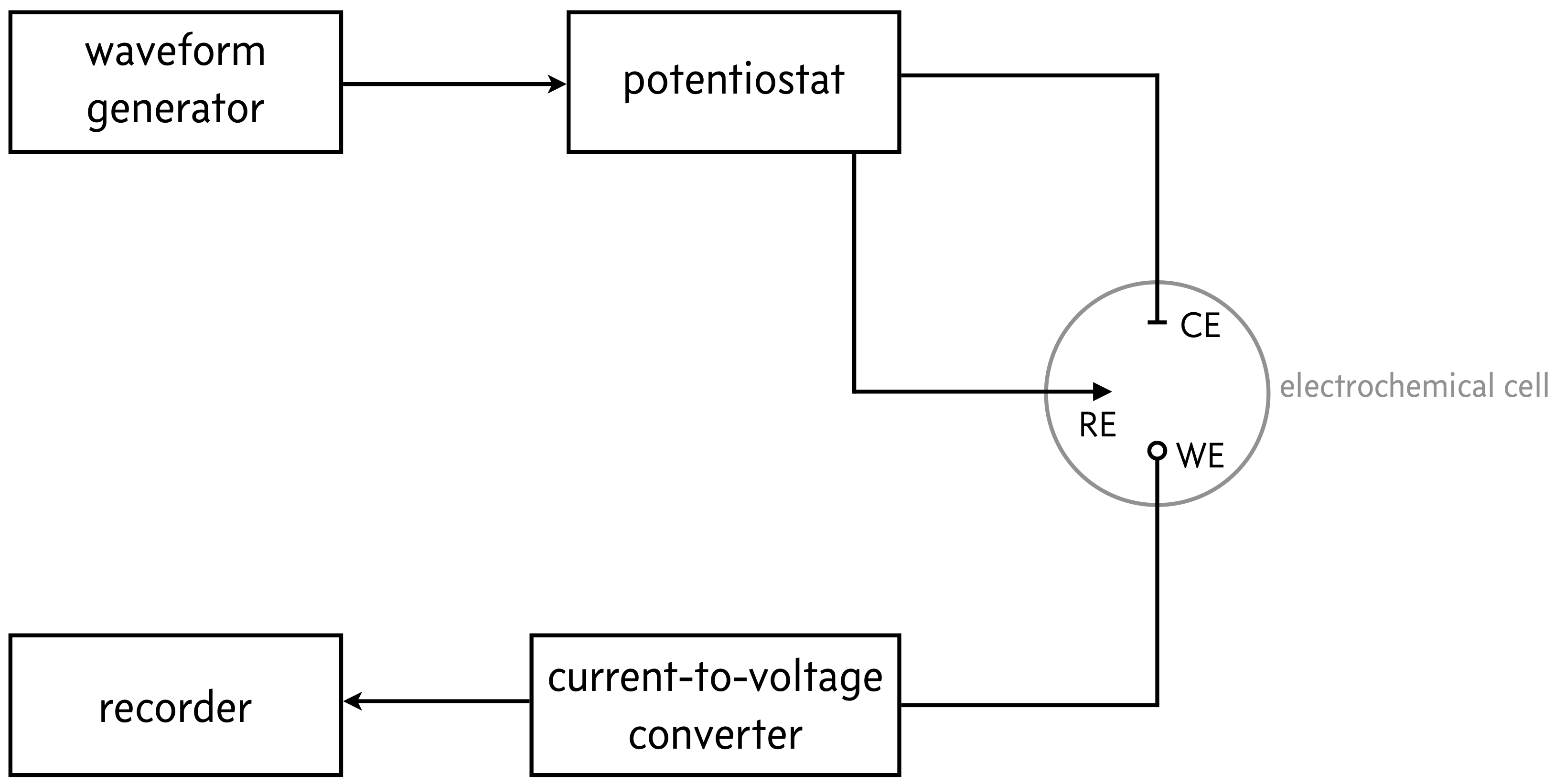
In the gray circle is the three-electrode electrochemical cell. Electrochemical cells are constructed to connect an analyte in solution to electrodes that can apply and measure voltages and currents. They are composed of a working electrode (WE), a reference electrode (RE), and a counter electrode (CE). A potential is appled at the working electrode, which is also the site of interest where, e.g., a redox reaction will take place. The reference electrode has a well-defined and stable equilibrium potential, so it provides a reference potential that the working electrode potential can be measured relative to. The counter electrode allows for a closed electrical circuit. Electrons flow between the WE and CE; as oxidation occurs at the WE, reduction occurs at the CE. The counter electrode must be sufficiently large so as not to limit the kinetics of the reaction.

A potentiostat is an electronic instrument that controls the voltage difference between a working and reference electrode. By controlling the potential, one can study charge transfer processes at the electrode-solution interface. The direction and rate of charge transfer can be thought of in terms of the measured current (charge transfer per time).

When studying redox reactions, the charge transfer occurs between the oxidized (Ox) and reduced (Re) species, \(\text{Ox} + n\,\text{e}^- \rightleftharpoons \text{Re}\), where \(n\) is the number of electrons transferred in the reduction reaction. If we think about voltage as the electron pressure applied by the power source, then we can think of this as the force which causes species in a redox reaction to gain or lose an electron (reduction or oxidation, respectively). Each chemical analyte has a specific redox potential at which the electron pressure overcomes the species’s electron affinity. Given a standard potential for the redox reaction, \(E^0\), we can describe the direction of a redox reaction based on applied potential \(E\) through the Nernst equation,

\[\begin{align} E = E^0 + \frac{k_BT}{ne}\,\ln \frac{c_\mathrm{ox}}{c_\mathrm{re}}, \end{align}\]

where \(k_BT\) is the thermal energy (with \(k_B = 1.38064852 \times 10^{-23}\) J/K being the Boltzmann constant), and \(e = 1.60217662 \times 10^{-19}\) A·s is the charge of single electron. According to the Nernst equation, when the applied potential is greater than the standard potential for the redox reaction, \(E > E^0\), the oxidized species is favored, and the reduced species is favored when \(E < E^0\).

Cyclic Voltammetry

In cyclic voltammetry (CV), the electrodes in the electochemical cell are stationary and the analyte solution is unstirred. The applied potential is in the shape of a triangle wave, usually for only one or two cycles.

CV is widely used in microbiology to study redox reactions that are part of metabolic processes. CV can also be used to detect and characterize analytes in bodily fluids like sweat, blood, saliva, and urine. Unstirred solutions stationary electrodes allow for simplicity of implementation for human-interfacing analysis. With the advent of screen printed carbon electrodes and laser engraving techniques, the electrochemical cells are thin and small, allowing for wearable biosensors using CV.

Upon application of a triangle wave potential, the current flowing between the working and counter electrode is measured, producing a trace of current versus applied potential. The plots below show the applied potential and current for a solution containing 2 mM hexacyanoferrate, which undergoes the reduction reaction

\[\begin{align} \text{Fe(CN)}_6^{3-} + \text{e}^- \rightleftharpoons \text{Fe(CN)}_6^{4-}. \end{align}\]

The data in the plots were aqcuired by Heather Lukas.

The blue sections of the plot are referred to as the “forward” scan and the orange sections the “reverse” scan. In the plots above, positive current is anodic, resulting from oxidation of the reduced species, \(\text{Re} \longrightarrow \text{Ox} + n\,\text{e}^-\). Negative current is cathodic, resulting from reduction of the oxidized species, \(\text{Ox} + n\,\text{e}^- \longrightarrow \text{Re}\).

Unfortunately, this convention, known as the IUPAC convention, is not universal, which can lead to great confusion. For example in the US convention the signs of the current are flipped, considering cathodic current as positive and anodic current as negative, which is the opposite of what I have shown in the above. The applied potential is also plotted with the axis flipped. So, when reading literature about CV, look carefully at axes and be sure you are clear on convention. In this project, please use the convention in the plots shown in this document.

“Duck” plots

The current and applied potential curves are typically plotted against each other, with applied potential on the x-axis and measured current on the y-axis, as shown below.

It is not a technical term, but I call these “duck plots” because the plot looks like a duck. This is not a technical term, but we will use it going forward here. The forward and reverse scans are typically not colored, but I color them here for clarity. Using our convention, the reverse scan lies below the forward scan.

A redox reaction is reversible if repeated traces of the I-V curves are identical; that is, the duck plots overlap. The redox reaction of hexacyanoferrate si reversible, as the traces almost exactly overlap. (The initial lack of overlap at 0.2 V is due to start-up effects in the experiment.) Repeated traces being shifted and nonoverlapping is a sign of irreversibility.

Diffusion-limited redox reactions

The rate of redox reactions, and thus the resulting current, can be limited by either mass transport (diffusion of redox species to the electrode surface) or charge transfer kinetics (determined by interactions between the specific reactant and electrode material). Many chemical reactions, and indeed the ones you will encounter in testing your device, are mass transport limited with fast electron transfer. To work out the kinetics, then, we need to describe the molecular flux \(\mathbf{j}(\mathbf{x}, t)\) of species.

The Nernst-Planck equation is a diffusion-advection-electromigration equation describing transport.

\[\begin{align} \mathbf{j}(\mathbf{x},t) = -D\,\nabla c - D\,\frac{ze}{k_BT}\,c\nabla \phi + \mathbf{u}c, \end{align}\]

where \(c(\mathbf{x},t)\) is the concentration of the ionic species of interest, \(D\) is the diffusion coefficient, \(z\) is the valence of the species, \(\phi\) is the electric potential, and \(\mathbf{u}\) is the fluid velocity. The resulting flux can show complex dynamics. In a CV experiment, the fluid is quiescent, so \(\mathbf{u} = 0\) and the reactions take place in a saline buffer, so \(\nabla \phi \approx 0\), meaning that the flux is entirely diffusive,

\[\begin{align} \mathbf{j}(\mathbf{x},t) \approx -D\,\nabla c. \end{align}\]

Thus, the current measured at the working electrode is given by the reaction rate, which is entirely dependent on the diffusive flux. The measured current \(i\) is therefore proportional to the concentration gradient at the working electrode. Assuming a radial symmetry about the working electrode, the diffusive flux is along one direction (radially), giving

\[\begin{align} i(t) = -n A j(r_0, t) = n A D\,\frac{\mathrm{d}c(r_0,t)}{\mathrm{d}r}, \end{align}\]

where \(r_0\) is the position of the electrode surface and \(A\) is its area.

With this in mind, let us now investigate what gives the duck curve its shape. Below is a plot of the second cycle of the above cyclic voltammograms with annotations.

We start the scan at point A, with a low applied potential. When the applied potential is low (or largely negative), conditions are such that the reduced species is thermodynamically favored, as per the Nernst equation. The oxidized species is enriched at the electrode, leading to a small gradient in oxidized species concentration. Meanwhile, the reduced species is depleted at the electrode and its concentration grows away from the electrode. As a result, there is a diffusive flux of oxidized species away from the electrode and a flux of reduced species toward it. This results in a slow rise in the anodic current; the rise is only slow because the oxidized state is still strongly favored. The current in this region of the trace is referred to as the capacitive current

At point B, the potential has gotten high enough where the oxidized species starts to be thermodynamically favored, and oxidation rate grows rapidly as the potential continues to increase toward point C. At point C, where oxidation is proceeding at maximal rate, the potential is referred to as the peak anodic potential, denoted \(E_{\mathrm{pa}}\). The current between points B and C of the trace is referred to as the Faradaic current.

Past point C until point D, even though oxidation is thermodynamically favored, the rate of oxidation at the electrode is slowed down because the oxidized species has accumulated at the electrode, leading to a wider concentration gradient, thereby slowing diffusive delivery of the reduced species to the electrode surface.

The potential at point D is called the switching potential, which is the peak of the triangular wave of applied potential. Moving from point D toward point E, we still have slow oxidation, even slower than between points C and D, because we are bringing the potential down. Eventually, the potential drops low enough the the reduced species is thermodynamically preferred, leading to peak cathodic current at point F where the reduction reaction proceeds with maximal speed. The potential where the cathodic current is maximal is called the peak cathodic potential, denoted \(E_{\mathrm{pc}}\). As the potential continues to drop, we again have a wide diffusive layer, reducing the diffusive flux of analyte to the electrode, thereby slowing the reaction rate that therefore the current.

Consider another annotated duck plot below.

Based on the shape of the duck plot, we can learn key features about the redox reaction. If the redox reaction is reversible, the difference between the anodic and cathodic peak potentials, called the peak-to-peak separation \(\Delta E_\mathrm{p}\), allows for calculation of the standard voltage. Halfway between these two peaks is \(E_{1/2}\), the point at which the concentrations of the oxidized and the reduced form are equal. Then, we can determine the standard potential according to the Nernst equation.

\[\begin{align} E^0 \approx E_{1/2} = E_{\mathrm{pa}} - \Delta E_\mathrm{p} / 2. \end{align}\]

The peak anodic and cathodic currents, respectively denoted \(i_{\mathrm{pa}}\) and \(i_{\mathrm{pc}}\), are also revealing. (Take careful note in the plot above that the peak currents are measured against a baseline capacitive current.) For a reversible reaction, \(i_{\mathrm{pa}} / i_{\mathrm{pc}} \approx 1\). Importantly, for a diffusion-limited, reversible redox reaction, the Randles-Ševčík equation relates \(i_{\mathrm{pa}}\) to important physical parameters of the system.

\[\begin{align} i_\mathrm{pa} = 0.4463\,n e A c \left(\frac{n e v D}{k_BT}\right)^{1/2}, \end{align}\]

where \(c\) is the bulk concentration of analyte, and \(v\) is the scan rate, given, e.g., in volts per second. Note that the prefactor is dimensionless (it derives from the solution to the Nernst-Planck equation). It is important to choose the units of all parameters must be consistent. It is useful to know that the dimension of each parameter in terms of fundamental dimensions mass (M), length (L), time (T), and electric current (I).

\(e\)	\(IT\)
\(A\)	\(L^2\)
\(c\)	\(L^{-3}\)
\(v\)	\(ML^2/IT^4\)
\(D\)	\(L^2/T\)
\(k_BT\)	\(ML^2/T^2\)

For example, one would get consistent units by choosing \(c\) to have units of number of particles per cubic meter, \(A\) to have units of square meters, \(v\) to have units of volts per second, \(D\) to have units of square meters per second, using \(k_B\) in units of Joules per Kelvin, and temperature in units of Kelvin.

One can determine the diffusion coefficient of the analyte (usually the oxidized and reduced forms have very similar diffusion coefficients) by performing multiple CV experiments for various scan rates with the total concentration of analyte held constant over the experiments. Performing a regression of \(i_\mathrm{pa}\) versus \(v\) according to the Randles-Ševčík equation has a single parameter, \(n e A c \sqrt{n e D/k_BT}\), from which \(D\) can be extracted.

Similarly, CV can be used to obtain the concentration of an analyte of known diffusion coefficient by again varying the scan rate and performing a regression of \(i_\mathrm{pa}\) versus \(c\).

More complicated CV curves

It is important to note that current versus voltage curves only have the duck shape in ideal conditions in which there is a single diffusion limited simple redox reaction. For multiple reactions, reactions that are not diffusion limited, reactions that result in molecular rearrangements beyond electron transfer, etc., the shape of the CV curves can vary qualitatively.

Specification

Your task is to construct a potentiostat capable of performing cyclic voltammetry across a working electrode. You will use a 3-electrode electrochemical cell built-in to the screen-printed carbon electrode number 110 Metrohm/DropSens. Your cyclic voltameter should have the following design characteristics.

It is operated from a computer with a dashboard. The dashboard should show a CV trace (current as a function of applied potential) and include a control panel that takes in scanning parameters and allows for live control of the plot (start, pause, stop).
You should be able to adjust scan parameters, such as scan rate, applied voltage range, and number of scans/cycles.
You may also wish to report relevant statistics like the observed anodic and cathodic peak voltages and currents (max/min observed peaks).
Your dashboard should have controls to download acquired traces for further analysis.

Demonstration

To demonstrate your functioning instrument, you will do the following.

Obtain a cyclic voltammogram of a solution containing a known concentration of vitamin C. From this voltammogram, determine if the oxidation of vitamin C is reversible.
Obtain a series of voltammograms for solutions of vitamin C with known concentrations to obtain a calibration for concentration determination. From this calibration, attempt to determine the diffusion coefficient for vitamin C. It helps to know that the oxidation reaction of vitamin C is \(\mathrm{C}_6\mathrm{H}_8\mathrm{O}_6 + 2\mathrm{H}_2\mathrm{O} \longrightarrow \mathrm{C}_6\mathrm{H}_6\mathrm{O}_6 + 2\mathrm{H}_3\mathrm{O}^+ + 2\mathrm{e}^-\) and that the working electrode of the DropSens SPCE is shaped like a disk and is four millimeters in diameter.
Use your instrument and the calibration curve you obtained to determine the concentration of a solution of vitamin C of unknown concentration.

Suggestions

Use of SPCEs

The screen-printed carbon electrode is composed of a carbon working and counter electrode and a silver reference electrode. See the diagram on this webpage for the electrode connections. Some important things to be careful of when using the electrodes:

They are reusable, but care should be taken to rinse the working electrode surface well with water. Dried on samples may contaminate the sample you are measuring.
Be careful not to scratch the electrode surface, A scratched surface will influence the conductive surface area and will impact your measurement. To avoid this, do not put a pipette tip direction on the surface. To dry the electrode, don’t apply pressure to the electrode surface. Either let the electrode air dry or use a kimwipe to blot and absorb the excess fluid.
They are durable, but they can snap if knocked while tightly in the connector.
Measurements should be made when the electrode is flat. It may be helpful to tape the connector and the electrode to the table.
Remember that for an electrochemical cell to function, the counter, reference, and working electrode must all be in solution. Make sure to fully cover each electrode with the droplet. The electrodes are designed to work with a 50 µL solution of analyte.

Staying tidy

Since we will be dealing with both liquids and electronics, it is imperative you have an organized work station. Make sure that there are separate areas for each on your table. Do not be shy of using long connectors to keep things separate.

Tips for building the potentiostat

When constructing the circuits for your potentiostat, you should keep the following in mind.

You probably want to use a follower to stabilize the output signal.
You will need to do a current-to-voltage conversion to read the voltage using either Arduino’s ADC or an ADC breakout board. To do so, consider a transimpedence amplifer (TIA), possibly with a capacitor to prevent ringing.
In creating your voltage sweep, you will need to provide negative voltages, so you will need to include some sort of adding or differencing circuit since the DAC you have will only provide positive voltages.
You should try to obtain as high resolution as possible in your voltage sweep. This means that you should use the 10-bit DAC as opposed to, e.g., using Arduino’s built-in 8-bit PWM with a low-pass filter.
Be sure you measure the applied voltage; do not just assume that what you send via the DAC is what is delivered.

Useful reading

You may wish to read the following references.

Elgrishi et al., J. Chem. Educ., 2018. This is a pedagogical guide for the background of CV.
Yomthiangthae, et al., New J. Chem., 2020. This paper discusses analysis of vitamin C and other analytes using SPCEs.

Parting wisdom

As a final suggestion, I want to remind you to think modularly. Draw out a block diagram with the various components (the electrodes and any amplifiers or filters) and think through your design before building.

It is also best to work incrementally. For example, first figure out how to provide a voltage scan. Then make sure you can vary the potential of the working electrode with appropriate stability of the reference electrode, possibly using a saline solution. Then make sure your TIA works. Etc.